Flexible beams tutorial
This tutorial briefly introduces two simple planar beams and how to work with them with utility functions. The python source code of the beam tutorial can be found at:
main/pythonDev/Examples/beamTutorial.py
The tutorial uses the GeometricallyExactBeam2D, which is a shear deformable Reissner-Timoshenko beam, and a thin cable ANCFCable2D, which represents a large deformation Bernoulli-Euler beam.
The model includes two highly flexible planar with length 2m, height 0.005m, width 0.01m, Young’s modulus 1e9N/m\(^2\) and density 2000kg/m\(^3\). The shear deformable beam is rigidly attached to ground and the cable is rigidly attached to a moving ground.
We first import necessary libraries and set up a mbs. Note that utilities also include pi, sin, cos and sqrt.
import exudyn as exu
from exudyn.utilities import *
import numpy as np
SC = exu.SystemContainer()
mbs = SC.AddSystem()
We define a set of beam parameters, discretization and geometry for both beam models.
numberOfElements = 16
L = 2 # length of pendulum
E=2e11 # steel
rho=7800 # elastomer
h=0.005 # height of rectangular beam element in m
b=0.01 # width of rectangular beam element in m
A=b*h # cross sectional area of beam element in m^2
I=b*h**3/12 # second moment of area of beam element in m^4
nu = 0.3 # Poisson's ratio
EI = E*I
EA = E*A
rhoA = rho*A
rhoI = rho*I
ks = 10*(1+nu)/(12+11*nu) # shear correction factor
G = E/(2*(1+nu)) # shear modulus
GA = ks*G*A # shear stiffness of beam
g = [0,-9.81,0] # gravity vector
positionOfNode0 = [0,0,0] # 3D vector
positionOfNode1 = [L,0,0] # 3D vector
Build geometrically exact 2D beam template (Timoshenko-Reissner), which includes all parameters In order to create beams, we usually need to create 2D rigid body nodes, create beam elements, add constraints and loads.
However, there is a utility function GenerateStraightBeam(...),
which conveniently does this for straight beams, including discretization, constraints and gravity.
First, we create a beam template, which includes all beam parameters (this could also be another beam type):
beamTemplate = Beam2D(nodeNumbers = [-1,-1], #added later
physicsMassPerLength=rhoA,
physicsCrossSectionInertia=rhoI,
physicsBendingStiffness=EI,
physicsAxialStiffness=EA,
physicsShearStiffness=GA,
physicsBendingDamping=0.02*EI,
visualization=VObjectBeamGeometricallyExact2D(drawHeight = h))
Now we use this template and call GenerateStraightBeam, which takes the nodal positions,
calculates according beam element lengths from discretization and could add constraints,
if fixedConstraintsNode0 or fixedConstraintsNode1 are not None.
beamData = GenerateStraightBeam(mbs, positionOfNode0, positionOfNode1,
numberOfElements, beamTemplate, gravity= g,
fixedConstraintsNode0=[1,1,1],
fixedConstraintsNode1=None)
We perform the same operations for ANCF cable elemente (Bernoulli-Euler), but in this case, we do not add constraints:
beamTemplate = Cable2D(nodeNumbers = [-1,-1], #added later
physicsMassPerLength=rhoA,
physicsBendingStiffness=EI,
physicsAxialStiffness=EA,
physicsBendingDamping=0.02*EI,
visualization=VCable2D(drawHeight = h))
cableData = GenerateStraightBeam(mbs, positionOfNode0, positionOfNode1,
numberOfElements, beamTemplate, gravity= g,
fixedConstraintsNode0=None,
fixedConstraintsNode1=None)
Now, we create a ground object and markers to attach cable with generic joint
oGround = mbs.CreateGround(referencePosition=[0,0,0])
mGround = mbs.AddMarker(MarkerBodyRigid(bodyNumber=oGround, localPosition=[0,0,0]))
mCable = mbs.AddMarker(MarkerNodeRigid(nodeNumber=cableData[0][0]))
As we like to move the cable relative to ground, we employ a simple user function which prescribes relative rotation and (corotated) translation in the joint:
def UFoffset(mbs, t, itemNumber, offsetUserFunctionParameters):
x = SmoothStep(t, 2, 4, 0, 0.5) #translate in local joint coordinates
phi = SmoothStep(t, 5, 10, 0, pi) #rotates frame of mGround
return [x, 0,0,0,0,phi]
Finally, we add the rigid joint (2D displacements and rotation around Z fixed) as GenericJoint. Note that for 2D objects, we may only fix \(X\)- and \(Y\)-translations, as well as the \(Z\)-rotation
mbs.AddObject(GenericJoint(markerNumbers=[mGround, mCable],
constrainedAxes=[1,1,0, 0,0,1],
offsetUserFunction=UFoffset,
visualization=VGenericJoint(axesRadius=0.01,
axesLength=0.02)))
As in the previous example, we just need to assemble and set up simulation parameters:
mbs.Assemble()
simulationSettings = exu.SimulationSettings()
tEnd = 10
stepSize = 0.005
simulationSettings.timeIntegration.numberOfSteps = int(tEnd/stepSize)
simulationSettings.timeIntegration.endTime = tEnd
simulationSettings.timeIntegration.verboseMode = 1
simulationSettings.solutionSettings.solutionWritePeriod = 0.005
simulationSettings.solutionSettings.writeSolutionToFile = True
simulationSettings.linearSolverType = exu.LinearSolverType.EigenSparse
simulationSettings.timeIntegration.newton.useModifiedNewton = True #for faster simulation
## add some visualization settings
SC.visualizationSettings.nodes.defaultSize = 0.01
SC.visualizationSettings.nodes.drawNodesAsPoint = False #show beam nodes
SC.visualizationSettings.bodies.beams.crossSectionFilled = True
Now start the solver with visualization and run the solution viewer afterwards, because simulation may be faster than you can follow:
SC.renderer.Start()
mbs.SolveDynamic(simulationSettings)
SC.renderer.Stop()
## visualize computed solution:
mbs.SolutionViewer()
The visualization window for the solution drawn at 6.5s is shown in Fig. 12.
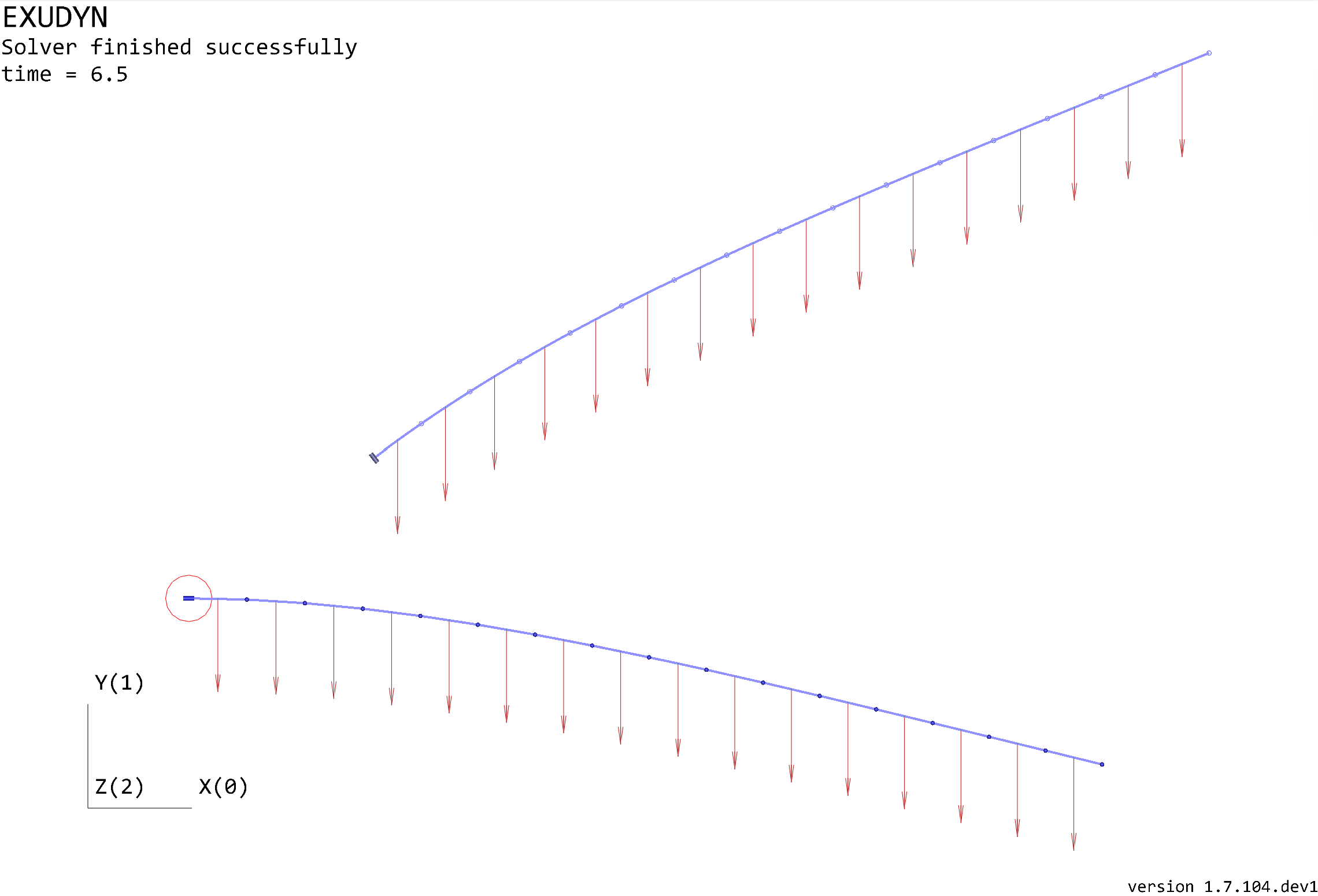
Fig. 12 Render window showing the deformed state of the two beams at 6.5s. The lower beam is fixed at the left end, while the upper beam’s support is translated and rotated.
This example should give you a good starting point to create beam models. See further examples, and more advanced functions, e.g., to create curved beam or reeving systems. There are also a sliding joint as well as axially moving beams and contact between beams and sheaves.
3D beams are still under development and include less functionality. In case, send a request at the GitHub discussion or issues.
clearpage