Solvers in Exudyn
The user has a couple of basic solvers available in Exudyn , see Fig. 31:
exudyn.SolveStatic(...): compute static solution for given problem (may also be used to compute kinematic behavior by prescribing joint motion)exudyn.SolveDynamic(...): time integration of equations of motionexudyn.ComputeLinearizedSystem(...): computes the linearized system of equations and returns mass, stiffness, damping matricesexudyn.ComputeODE2Eigenvalues(...): computes the eigenvalues of the linearized system of equations; only possible if no algebraic constraints in system; uses scipy to compute eigenvalues
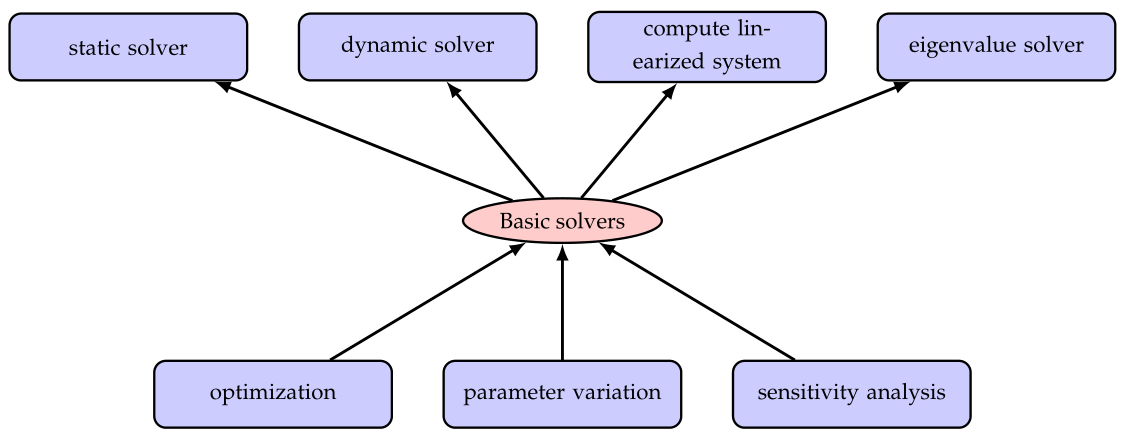
Fig. 31 Basic and advanced solvers in Exudyn ; advanced solvers build upon any basic solver to perform more sophisticated operations
There are advanced solvers, like in exudyn.processing:
Optimization:
GeneticOptimization(...): find optimum for given set of parameter ranges using genetic optimization; works in parallelMinimize(...): find optimum withscipy.optimize.minimize(...)ParameterVariation(...): compute a series of simulations for given set(s) of parameters; works in parallelComputeSensitivities(...): compute sensitivities for certain parameters; works in parallel
The advanced methods are build upon the basic solvers and essentially run single simulations in the background, see the according examples.
The basic solvers need a MainSystem, usually denoted as mbs, to be solved. Furthermore, a couple of options are usually to be given, which are explained shortly:
simulationSettings: This is a big structure, containing all solver options; note that only the according options forstaticSolverortimeIntegrationare used. Look at the detailed description of these options in Section Simulation settings. These settings influence the output rate and output quantity of the solution, solver reporting, accuracy, solver type, etc. Specifically, theverboseModemay be increased (2-4) to see the behavior of the solver and intermediate quantities.solverType: Only forexudyn.SolveDynamic(...): This is a simpler access to the solverType given in the internal structure oftimeIntegration.generalizedAlphaandsimulationSettings.timeIntegration.explicitIntegration.dynamicSolverType.
The function exudyn.SolveDynamic(...) sets the according variables internally. For available solver types, see the description of exudyn.DynamicSolverType in Section DynamicSolverType.
storeSolver: ifTrue, the solver is stored inmbs.sys['staticSolver']ormbs.sys['dynamicSolver']and also solver settings are stored inmbs.sys['simulationSettings']. After the solver has finished,mbs.sys['staticSolver']can be used to retrieve additional information on convergence, system matrices, etc. (see the solver structure).showHints: This shows a lot of possible solutions in case of no convergenceshowCausingItems: This shows a potential causing item if the linear solver failed; the item number is computed from the coordinate number that caused problems (e.g., a row that became zero during factorization); note that this item may not be the real cause in your problem
System equations of motion
The system equations of motion in Exudyn follow the notations of Section Nomenclature for system equations of motion and solvers and are represented as
Here, we introduce different Lagrange multipliers \(\tlambda_q\) and \(\tlambda_{\dot q}\) which have equal sizes as \(\tlambda\), while those \(\lambda_i\) which belong to holonomic constraints, are included in \(\tlambda_q\) and \(\tlambda_i\) belonging to non-holonomic constraints, are included in \(\tlambda_{\dot q}\), whereas other components in \(\tlambda_q\) or \(\tlambda_{\dot q}\) are zero.
It may help to know that for linear mechanical the term \({\mathbf{f}}_\SO\) becomes
in which \({\mathbf{f}}^a\) represents applied forces and stiffness matrix \({\mathbf{K}}\) and damping matrix \({\mathbf{D}}\) become part of the system Jacobian for time integration.