ObjectContactSphereSphere

[UNDER CONSTRUCTION] A simple contact connector between two spheres. The connector implements at least the same functionality as in GeneralContact and is intended for simple setups and for testing, while GeneralContact is much more efficient due to parallelization approaches and efficient contact search.

Authors: Gerstmayr Johannes, Weyrer Sebastian

Additional information for ObjectContactSphereSphere:

  • This Object has/provides the following types = Connector
  • Requested Marker type = Position + Orientation
  • Requested Node type = GenericData

The item ObjectContactSphereSphere with type = ‘ContactSphereSphere’ has the following parameters:

  • name [type = String, default = ‘’]:
    constraints’s unique name
  • markerNumbers [\([m0,m1]\tp\), type = ArrayMarkerIndex, size = 2, default = [ invalid [-1], invalid [-1] ]]:
    list of markers representing centers of spheres, used in connector
  • nodeNumber [\(n_d\), type = NodeIndex, default = invalid (-1)]:
    node number of a NodeGenericData with numberOfDataCoordinates = 4 dataCoordinates, needed for discontinuous iteration (friction and contact); data variables contain values from last PostNewton iteration: data[0] is the gap, data[1] is the norm of the tangential velocity (and thus contains information if it is stick or slip); data[2] is the impact velocity; data[3] is the plastic overlap of the Edinburgh Adhesive Elasto-Plastic Model, initialized usually with 0 and set back to 0 in case that spheres have been separated.
  • spheresRadii [\([r_0,r_1]\tp\), type = Vector2D, size = 2, default = [-1.,-1.]]:
    Vector containing radius of sphere 0 and radius of sphere 1 [SI:m]
  • dynamicFriction [\(\mu_d\), type = UReal, default = 0.]:
    dynamic friction coefficient for friction model, see StribeckFunction in exudyn.physics, Section Module: physics
  • frictionProportionalZone [\(v_{reg}\), type = UReal, default = 1e-3]:
    limit velocity [m/s] up to which the friction is proportional to velocity (for regularization / avoid numerical oscillations), see StribeckFunction in exudyn.physics (named regVel there!), Section Module: physics
  • contactStiffness [\(k_c\), type = UReal, default = 0.]:
    normal contact stiffness [SI:N/m] (units in case that \(n_\mathrm{exp}=1\))
  • contactDamping [\(d_c\), type = UReal, default = 0.]:
    linear normal contact damping [SI:N/(m s)]; this damping should be used (!=0) if the restitution coefficient is < 1, as it changes its behavior.
  • contactStiffnessExponent [\(n_\mathrm{exp}\), type = PReal, default = 1.]:
    exponent in normal contact model [SI:1]
  • constantPullOffForce [\(f_\mathrm{adh}\), type = UReal, default = 0.]:
    constant adhesion force [SI:N]; Edinburgh Adhesive Elasto-Plastic Model
  • contactPlasticityRatio [\(\lambda_\mathrm{P}\), type = UReal, default = 0.]:
    ratio of contact stiffness for first loading and unloading/reloading [SI:1]; Edinburgh Adhesive Elasto-Plastic Model; \(\lambda_\mathrm{P}=1-k_c/K2\), which gives the contact stiffness for unloading/reloading \(K2 = k_c/(1-\lambda_\mathrm{P})\); set to 0 in order to fully deactivate Edinburgh Adhesive Elasto-Plastic Model model
  • adhesionCoefficient [\(k_\mathrm{adh}\), type = UReal, default = 0.]:
    coefficient for adhesion [SI:N/m] (units in case that \(n_\mathrm{adh}=1\)); Edinburgh Adhesive Elasto-Plastic Model; set to 0 to deactivate adhesion model
  • adhesionExponent [\(n_\mathrm{adh}\), type = UReal, default = 1.]:
    exponent for adhesion coefficient [SI:1]; Edinburgh Adhesive Elasto-Plastic Model
  • restitutionCoefficient [\(e_\mathrm{res}\), type = PReal, default = 1.]:
    coefficient of restitution [SI:1]; used in particular for impact mechanics; different models available within parameter impactModel; the coefficient must be > 0, but can become arbitrarily small to emulate plastic impact (however very small values may lead to numerical problems)
  • minimumImpactVelocity [\(\dot\delta_\mathrm{-,min}\), type = UReal, default = 0.]:
    minimal impact velocity for coefficient of restitution [SI:1]; this value adds a lower bound for impact velocities for calculation of viscous impact force; it can be used to apply a larger damping behavior for low impact velocities (or permanent contact)
  • impactModel [\(m_\mathrm{impact}\), type = UInt, default = 0]:
    number of impact model: 0) linear model (only linear damping is used); 1) Hunt-Crossley model; 2) Gonthier/EtAl-Carvalho/Martins mixed model; model 2 is much more accurate regarding the coefficient of restitution, in the full range [0,1] except for 0; NOTE: in all models, the linear contactDamping still added, if not set to zero!
  • activeConnector [type = Bool, default = True]:
    flag, which determines, if the connector is active; used to deactivate (temporarily) a connector or constraint
  • visualization [type = VObjectContactSphereSphere]:
    parameters for visualization of item

The item VObjectContactSphereSphere has the following parameters:

  • show [type = Bool, default = False]:
    set true, if item is shown in visualization and false if it is not shown; draws spheres by given radii
  • color [type = Float4, default = [0.7,0.7,0.7,1.]]:
    RGBA connector color; if R==-1, use default color

DESCRIPTION of ObjectContactSphereSphere

The following output variables are available as OutputVariableType in sensors, Get…Output() and other functions:

  • Director3:
    contains normalized vector from marker 0 to marker 1
  • Displacement:
    global displacement vector between the two spheres midpoints
  • DisplacementLocal:
    3D Vector, containing only gap (Z-component)
  • Velocity:
    global relative velocity between the two spheres midpoints
  • Force:
    global contact force vector
  • Torque:
    global torque due to friction on marker 0; to obetain torque on marker 1, multiply the torque with the factor \(\frac{r_1+g/2}{r_0+g/2}\)

Definition of quantities

intermediate variables
symbol
description
marker m0 position
\(\LU{0}{{\mathbf{p}}}_{m0}\)
global position of sphere 0 center as provided by marker m0
marker m0 orientation
\(\LU{0,m0}{\Rot}\)
current rotation matrix provided by marker m0
marker m1 position
\(\LU{0}{{\mathbf{p}}}_{m1}\)
global position of sphere 1 center as provided by marker m1
marker m1 orientation
\(\LU{0,m1}{\Rot}\)
current rotation matrix provided by marker m1
data coordinates
\({\mathbf{x}}=[x_0,\,x_1,\,x_2,\,x_3]\tp\)
hold the current gap (0), the (norm of the) tangential velocity (1), the impact velocity (2), and the plastic deformation (3) of the adhesion model
marker m0 velocity
\(\LU{0}{{\mathbf{v}}}_{m0}\)
current global velocity which is provided by marker m0
marker m1 velocity
\(\LU{0}{{\mathbf{v}}}_{m1}\)
current global velocity which is provided by marker m1
marker m0 angular velocity
\(\LU{0}{\tomega}_{m0}\)
current angular velocity vector provided by marker m0
marker m1 angular velocity
\(\LU{0}{\tomega}_{m1}\)
current angular velocity vector provided by marker m1

Connector Forces

This section outlines the computation of the forces acting on the two spheres when they are in contact with each other. Two types of forces can act on the spheres due to the connector:

  • normal force computed according to the chosen impact model \(m_\mathrm{impact}\) and with contact damping if \(d_c\neq0\); this type of force does not create a torque acting on the spheres.

  • tangential force due to a regularized friction law to model dry friction between the spheres; this type of force creates a torque acting on the spheres and is computed independently of the chosen impact model if \(\mu_d\neq0\) is set. Note that in the implemented model, rolling deformations are not considered, i.e. the friction is only a function of the relative tangential velocity between the spheres at the contact point.

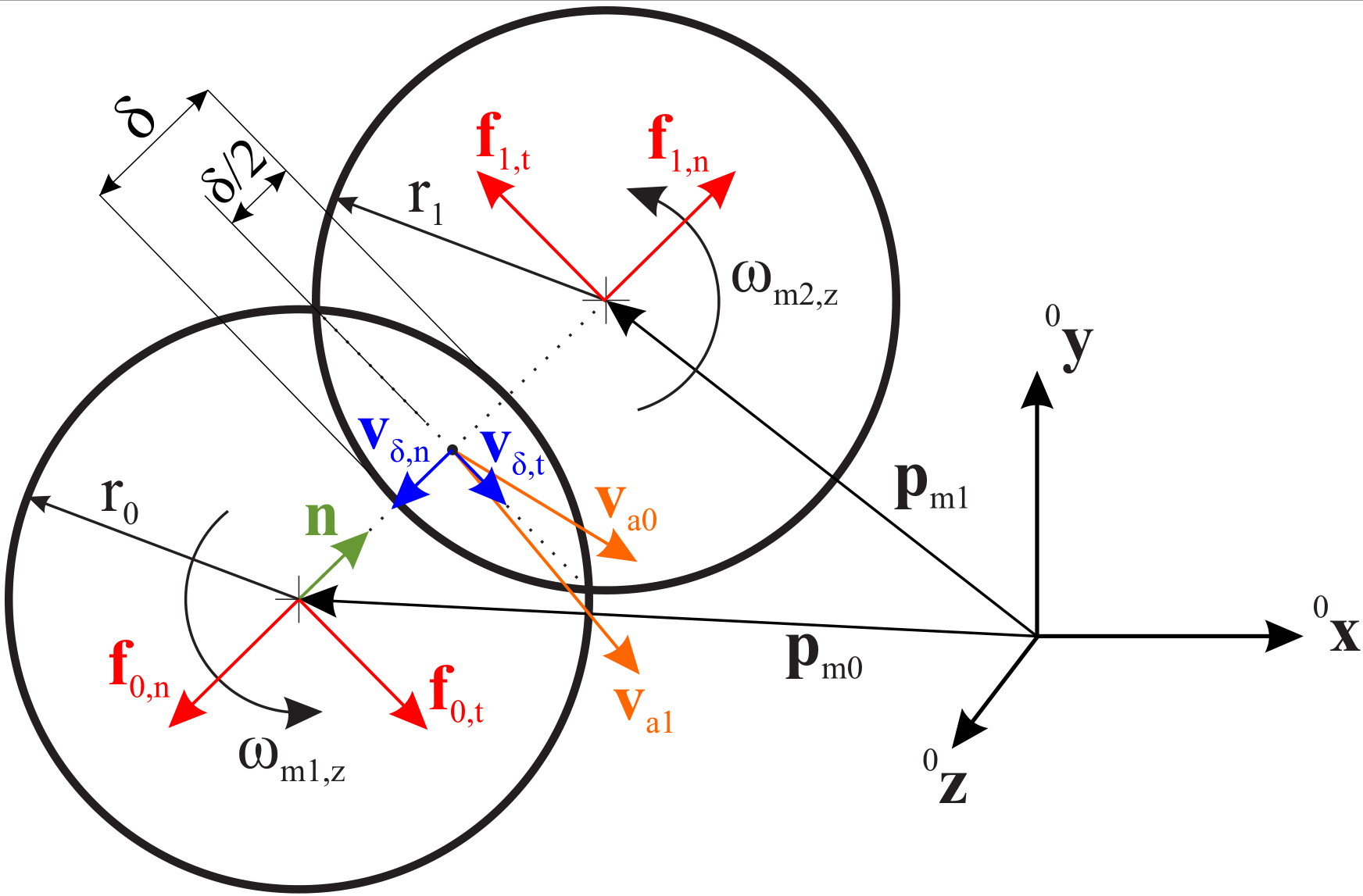
../../../_images/SphereSphereContact.png

Fig. 46 Two spheres that are in contact, showing a force on marker 1 in normal direction due to overlap; forces on marker 0 act in opposite direction.

For the following, the gap \(g\) between the two spheres is computed as

\[g = || \LU{0}{{\mathbf{p}}}_{m1} - \LU{0}{{\mathbf{p}}}_{m0} || - (r_0 + r_1)\]

and the overlap \(\delta\) is the negated gap: \(\delta=-g\). In the contact case, the overlap \(\delta\) is positive. The normal vector \(\LU{0}{{\mathbf{n}}}\) points from marker 0 to marker 1 and is computed with

\[\LU{0}{{\mathbf{n}}} = \frac{\LU{0}{{\mathbf{p}}}_{m1} - \LU{0}{{\mathbf{p}}}_{m0}}{|| \LU{0}{{\mathbf{p}}}_{m1} - \LU{0}{{\mathbf{p}}}_{m0} ||} .\]

The scalar normal (gap) velocity \(v_\mathrm{\delta,n}\) is computed with the velocities \(\LU{0}{{\mathbf{v}}}_{m0}=\LU{0}{\dot{{\mathbf{p}}}}_{m0}\) and \(\LU{0}{{\mathbf{v}}}_{m1}=\LU{0}{\dot{{\mathbf{p}}}}_{m1}\)

\[v_\mathrm{\delta,n} = \left(\LU{0}{{\mathbf{v}}}_{m1} - \LU{0}{{\mathbf{v}}}_{m0}\right)\cdot \LU{0}{{\mathbf{n}}}\]

and the tangential (gap) velocity \(\LU{0}{{\mathbf{v}}}_\mathrm{\delta,t}\) at the contact point, that is needed for the friction model, reads

(84)\[\LU{0}{{\mathbf{v}}}_\mathrm{\delta,t} = \left(\LU{0}{{\mathbf{v}}}_{a1} - \LU{0}{{\mathbf{v}}}_{a0}\right) - v_\mathrm{\delta,n} \cdot \LU{0}{{\mathbf{n}}}, \qquad v_\mathrm{rel} = || \LU{0}{{\mathbf{v}}}_\mathrm{\delta,t} || .\]

To take the angular velocity of the spheres into account, the velocities \(\LU{0}{{\mathbf{v}}}_{a0}\) and \(\LU{0}{{\mathbf{v}}}_{a1}\) at the contact point are computed using Euler’s theorem for kinematics:

\[\LU{0}{{\mathbf{v}}}_{a0} = \LU{0}{{\mathbf{v}}}_{m0} + \LU{0}{\tomega}_{m0} \times \left(\LU{0}{{\mathbf{n}}}\cdot \left(r_0-\frac{\delta}{2}\right)\right) , \qquad \LU{0}{{\mathbf{v}}}_{a1} = \LU{0}{{\mathbf{v}}}_{m1} + \LU{0}{\tomega}_{m1} \times \left(-\LU{0}{{\mathbf{n}}}\cdot \left(r_1-\frac{\delta}{2}\right)\right) .\]

The normal force acting on marker 1 is generally written as

\[\LU{0}{{\mathbf{f}}}_\mathrm{1,n} = \underbrace{(f_c + f_d)}_{f_\mathrm{1,n}} \cdot \LU{0}{{\mathbf{n}}} ,\]

where \(f_c\) is the elastic and \(f_d\) the damping part. The damping \(f_d\) is always computed the same, independent of the chosen impact model:

\[f_d = - d_c v_\mathrm{\delta,n} .\]

The negative sign is because of the damping acting against the gap velocity: in the case of a positive normal (gap) velocity, the damping acts against \(\LU{0}{{\mathbf{n}}}\) for marker 1. The elastic force \(f_c\) is computed depending on the chosen impact model.

  • \(m_\mathrm{impact}=0\): the Adhesive Elasto-Plastic model described in is used. This model captures the key bulk behavior of cohesive powders and granular soils. For the impact model, the plastic overlap \(\delta_p\) is needed. It is computed with

\[ \begin{align}\begin{aligned} \delta_p=\lambda_\mathrm{p}^{\frac{1}{n_\mathrm{exp}}}\delta .\\ The Adhesive Elasto-Plastic model distinguishes three different cases, modeling the loading and unloading behavior of the spheres:\end{aligned}\end{align} \]
\[\begin{split}f_c= \begin{cases} -f_\mathrm{adh} + k_c \delta^{n_\mathrm{exp}} & \text{if } k_2 \left(\delta^{n_\mathrm{exp}}-\delta_p^{n_\mathrm{exp}} \right) \geq k_c\delta^{n_\mathrm{exp}} \\ -f_\mathrm{adh} + k_2 \left(\delta^{n_\mathrm{exp}}-\delta_p^{n_\mathrm{exp}} \right) & \text{if } k_c\delta^{n_\mathrm{exp}} > k_2 \left(\delta^{n_\mathrm{exp}}-\delta_p^{n_\mathrm{exp}}\right) > -k_\mathrm{adh}\delta^{n_\mathrm{adh}} \\ -f_\mathrm{adh}-k_\mathrm{adh}\delta^{n_\mathrm{adh}} & \text{if } -k_\mathrm{adh}\delta^{n_\mathrm{adh}} > k_2 \left(\delta^{n_\mathrm{exp}}-\delta_p^{n_\mathrm{exp}} \right) \end{cases} .\end{split}\]

Note that \(k_2\) is computed with \(k_2 = k_c/(1-\lambda_\mathrm{P})\). The terms with the stiffness \(k_c\) and \(k_2\) have a positive sign, since they act in the direction of \(\LU{0}{{\mathbf{n}}}\) for marker 1. The constant adhesion force \(f_\mathrm{adh}\) and the stiffness \(k_\mathrm{adh}\) act against \(\LU{0}{{\mathbf{n}}}\), which corresponds to a force sticking the spheres together.

  • \(m_\mathrm{impact}=1\): the restitution model proposed by Hunt and Crossley in is used to simulate the energy loss of the spheres during contact:

\[ \begin{align}\begin{aligned} f_c=k_c \delta^{n_\mathrm{exp}} + \lambda \delta^{n_\mathrm{exp}} v_\mathrm{\delta,n}\\ with\end{aligned}\end{align} \]
\[ \begin{align}\begin{aligned} \lambda = \frac{k_c}{\dot\delta_\mathrm{-}}\frac{3}{2}(e_\mathrm{res}-1) .\\ The restitution coefficient \ :math:`e_\mathrm{res}`\ describes the ration of the normal (gap) velocity before and after the impact of the spheres. In the case of \ :math:`e_\mathrm{res}<1`\ , the impact has a plastic portion, resulting in a force acting against \ :math:`\LU{0}{{\mathbf{n}}}`\ for marker 1, which is why \ :math:`\lambda`\ must be negative in that case. \ :math:`\dot\delta_\mathrm{-}`\ is the initial relative velocity, which is either the minimum impact velocity or the normal (negated gap) velocity:\end{aligned}\end{align} \]
\[\dot\delta_\mathrm{-} = \max{\left(\dot\delta_\mathrm{-,min}; -v_\mathrm{\delta,n} \right)}\]

Note that the Hunt-Crossley restitution is valid for a very small energy loss (\(e_\mathrm{res}\approx1\)) .

  • \(m_\mathrm{impact}=2\): a generalization of the Hunt-Crossley restitution proposed by Carvalho and Martins in is used for \(e_\mathrm{res} > \frac{1}{3}\) and a model proposed by Gonthier et al. in is used for impacts with a high plastic proportion, \(e_\mathrm{res} < \frac{1}{3}\). Note that the two models are identical at \(e_\mathrm{res} = \frac{1}{3}\). \(\lambda\) is therefore computed as follows:

\[\begin{split}\lambda= \begin{cases} \frac{k_c}{\dot\delta_\mathrm{-}}\frac{3}{2}(e_\mathrm{res}-1)\frac{11-e_\mathrm{res}}{1+9e_\mathrm{res}} & \text{if } e_\mathrm{res} > \frac{1}{3} \\ \frac{k_c}{\dot\delta_\mathrm{-}}\frac{e_\mathrm{rep}^2-1}{e_\mathrm{rep}} & \text{if } e_\mathrm{res} > 0 \\ \end{cases} .\end{split}\]

The tangential force acting on marker 1 due to the friction model acts against the tangential velocity \({\mathbf{v}}_\mathrm{\delta,t}\), see the computation of \({\mathbf{v}}_\mathrm{\delta,t}\) in Equation (84). Thus, the tangential force for marker 1 is computed as

\[\begin{split}\LU{0}{{\mathbf{f}}}_\mathrm{1,t} = -\LU{0}{{\mathbf{v}}}_\mathrm{\delta,t} \cdot \begin{cases} \frac{\mu_d f_\mathrm{1,n}}{v_{reg}} & \text{if } v_{rel} < v_{reg} \\ \frac{\mu_d f_\mathrm{1,n}}{v_{rel}} & \text{else}\\ \end{cases} .\end{split}\]

Note that the case distinction above is made to ensure that for very small relative velocities the friction force does not become implausibly high. Taken together, the force acting on marker 1 due to the connector is computed as

\[\LU{0}{{\mathbf{f}}}_{m1}=\LU{0}{{\mathbf{f}}}_\mathrm{1,n}+\LU{0}{{\mathbf{f}}}_\mathrm{1,t} ,\]

the force acting on marker 0 is \(\LU{0}{{\mathbf{f}}}_{m0}=-\LU{0}{{\mathbf{f}}}_{m1}\). The global torque \(\LU{0}{\ttau}_{m1}\) acting on marker 1 due to the connector is computed as

\[\LU{0}{\ttau}_{m1}=-\LU{0}{{\mathbf{n}}}\left( r_1-\frac{1}{2}\delta \right) \times \LU{0}{{\mathbf{f}}}_{m1} ,\]

and on marker 0 as

\[\LU{0}{\ttau}_{m0}=\LU{0}{{\mathbf{n}}} \left(r_0-\frac{1}{2}\delta \right) \times \LU{0}{{\mathbf{f}}}_{m0}= \LU{0}{{\mathbf{n}}}\left( r_0-\frac{1}{2}\delta \right) \times -\LU{0}{{\mathbf{f}}}_{m1} .\]

It can be seen that the torque due to the connector is the same for both spheres, if \(r_0=r_1\) applies.

Relevant Examples and TestModels with weblink:

The web version may not be complete. For details, consider also the Exudyn PDF documentation : theDoc.pdf